重心是三角形三条中线的交点。当几何体为匀质物体时,重心与形心重合。

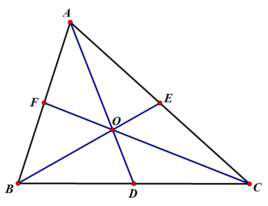
三角形重心是三角形三边每一边的三条中线的交点。当几何体为匀质物体时,重心与形心重合。三条中线必相交,交点命名为重心;重心分割中线段,线段之比二比一。三角形重心的性质:
1、重心到顶点的距离与重心到对边中点的距离之比为2:1。
2、重心和三角形3个顶点组成的3个三角形面积相等。
3、重心到三角形3个顶点距离平方的和最小。(等边三角形)
4、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数,即其坐标为[(x1 x2 x3)/3,(y1 y2 y3)/3];空间直角坐标系——x坐标:(x1 x2 x3)/3,y坐标:(y1 y2 y3)/3,z坐标:(z1 z2 z3)/3。

5、三角形内到三边距离之积最大的点。
6、在△abc中,若ma向量 mb向量 mc向量=0(向量),则m点为△abc的重心,反之也成立。
7、设△abc重心为g点,所在平面有一点o,则向量og=1/3(向量oa 向量ob 向量oc)。
8、卡诺重心定理:若g为三角形abc的重心,p为三角形abc所在平面上任意一点,则pa^2 pb^2 pc^2=ga^2 gb^2 gc^2 3pg^2=1/3(a^2 b^2 c^2) 3pg^2。